January 2, 2009
The New Math
Ron Eglash’s discovery of fractals in African architecture spurred a rewriting of math curriculum and a fresh take on design.
A modern-day example of fractals in an African Village: a design sketch for a new community center in Zambia. Image courtesy of Ron Eglash.
We often hear about how the organic forms of nature inform design, but what about the complex repetitions of a mathematical pattern? Ron Eglash, an associate professor at Rensselaer Polytechnic Institute in Troy, New York, was surprised to discover that many African villages traditionally organized their buildings in a complex geometric pattern known as a fractal, or a series of ever-diminishing similarly-shaped curves. Fractals had been considered a relatively modern mathematical discovery, and the geometric pattern was most frequently employed in computer graphics, so it was a revelation to learn that indigenous design included such seemingly contemporary shapes.
Eglash made the discovery when his research about technology in the third world led him to an anthropologist studying a village in Tanzania. “The women of this village had a lot of autonomy,” Eglash explains today. “In Islamic culture, they could get a divorce by building their own house. They were using the architecture as a way to assert their rights.” A modernization program was coming to the village and the anthropologist worried that the new housing plan would effectively destroy this tradition. “The new geometry of the village was going to be a grid, like most European or American cities. But I couldn’t understand the way the village was originally organized so I wrote to her and asked her for aerial photos.” That’s when Eglash saw the unmistakable geometry of the fractal.
The discovery led Eglash to a broader study of design in Africa and he learned that fractals were employed in everything from basket weaving to hair braiding. He expanded his research to include other indigenous cultures, such as Native Americans, where he uncovered the ways in which mathematical computations were applied to everyday design.
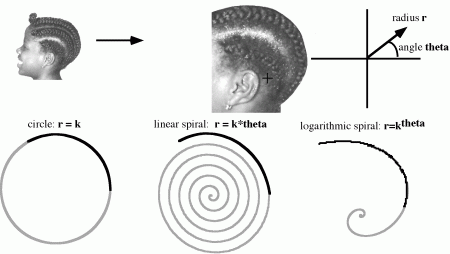
Analysis of a cornrow curve. Courtesy of Ron Eglash.
Today, Eglash uses his research as a basis for middle school math curricula. He developed culturally-situated design tools that help teach kids about math through their own visual environment. There’s a course on cornrows, which uses a software applet to introduce kids to fractal geometry. There’s the Graffiti Grapher, which teaches about cartesian and polar coordinate geometry in graffiti. The Virtual Breakdancer invites students to create their own online breakdance (while learning about rotation and sine function).
Eglash is working to bring these courses into the classroom. “Using culture in the math classroom isn’t intuitive to teachers and unless they are already attuned, it’s hard to get a foot in the door,” he admits. “But once we’ve shown teachers how to use the software, it’s been a big success.”
Eglash recently encouraged a class to come up with its own software tool to create personalized skateboards. He hopes that this melding of culture, math, and design will help students recognize their own potential as creators. “One of the things that needs to shift with these kids is getting them to think of themselves as producers and getting them to realize the pride you can have in your own productions.”





